Facility location
Facility location, also known as location analysis, is a branch of operations research and computational geometry concerning itself with mathematical modeling and solution of problems concerning optimal placement of facilities in order to minimize transportation costs, avoid placing hazardous materials near housing, outperform competitors' facilities, etc.
Contents |
Minsum facility location
A simple facility location problem is the Fermat-Weber problem, in which a single facility is to be placed, with the only optimization criterion being the minimization of the sum of distances from a given set of point sites. More complex problems considered in this discipline include the placement of multiple facilities, constraints on the locations of facilities, and more complex optimization criteria.
In a basic formulation, the Facility Location problem consists of a set of potential facility sites L where a facility can be opened, and a set of demand points D that must be serviced. The goal is to pick a subset F of facilities to open, to minimize the sum of distances from each demand point to its nearest facility, plus the sum of opening costs of the facilities.
The Facility Location problem on general graphs is NP-hard to solve optimally, by reduction from (for example) the Set Cover problem. A number of approximation algorithms have been developed for the facility location (FP) problem and many of its variants.
Without assumptions on the set of distances between clients and sites (in particular, without assuming that the distances satisfy the triangle inequality), the problem is known as Non-Metric Facility Location and is approximable within a factor O(log(n)).[1] This factor is tight, via an approximation-preserving reduction from the Set Cover problem.
If we assume distances between clients and sites are undirected and satisfy the triangle inequality, we are talking about a Metric Facility Location problem (MFL). The MFL is still NP-hard and hard to approximate within factor better than 1.46. The currently best known approximation algorithm achieves approximation ratio of 1.488.[2]
Minimax facility location
The minimax facility location problem seeks a location which minimizes the maximum distance to the sites.
In the case of the Euclidean metric, it is known as the smallest enclosing sphere problem or 1-center problem. Its study traced a least to the year of 1860. The planar case (smallest enclosing circle problem) may be solved in optimal time 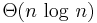 .[3]
.[3]
Maxmin facility location
The maxmin facility location or obnoxious facility location problem seeks a location which maximizes the minimum distance to the sites. In the case of the Euclidean metric, it is known as the largest empty sphere problem. The planar case (largest empty circle problem) may be solved in optimal time 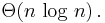 [3][4]
[3][4]
See also
References
- ^ D. S. Hochbaum. Heuristics for the fixed cost median problem. Math. Programming, 22:148-162, 1982.
- ^ Shi Li. A 1.488-approximation algorithm for the uncapacitated facility location problem. International Colloquium on Automata, Languages and Programming (ICALP), pages 77-88, 2011 [1]
- ^ a b Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6., p. 256
- ^ G. T. Toussaint, "Computing largest empty circles with location constraints," International Journal of Computer and Information Sciences, vol. 12, No. 5, October, 1983, pp. 347-358.
External links
- INFORMS section on location analysis, a professional society concerned with facility location.
- Bibliography on facility location collected by Trevor Hale, containing over 3400 articles.
- Library of location algorithms
- Web-based facility location utility (single facility)